| quest'ultima relazione ha due soluzioni: |
|
e |
|
|
DE SECTIO AUREA - IN MATEMATICA |
Per analogia con la Geometria, dato un numero n si tratta di trovare il medio proporzionale x tra il numero dato e la sua differenza n-x. In pratica bisogna risolvere l'equazione:
n : x = x : (n-x)
| da cui si ottiene: | x2 = n2 – nx |
| e quindi: | x2 + nx - n2 = 0 |
| quest'ultima relazione ha due soluzioni: |
|
e |
|
scartando
la soluzione negativa si ricava che il rapporto tra il medio proporzionale x
ed il numero n è una costante che vale: ![]()
e che, ovviamente, è un numero irrazionale. Viceversa il rapporto tra il numero n e il medio proporzionale x vale:
![]()
La
denominazione di Rapporto Aureo viene talora data alla prima (![]() ),
talora alla seconda (
),
talora alla seconda (![]() ). E' facile
mostrare che tra le due vale la relazione:
). E' facile
mostrare che tra le due vale la relazione: ![]()
| Vale altresì la relazione: | 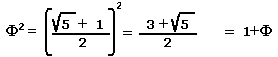 |
ovvero: | |
|
e quindi: |
|||
Cioè
![]() ha il valore della cosiddetta
radice continua.
ha il valore della cosiddetta
radice continua.
E’
facile anche mostrare che, per una nota proprietà delle proporzioni, la
differenza![]() è in rapporto
aureo con x, e che
è in rapporto
aureo con x, e che![]() . Graficamente
possiamo rappresentare così le relazioni tra 1, r,
. Graficamente
possiamo rappresentare così le relazioni tra 1, r,
![]() e
e ![]() :
:
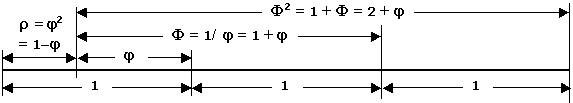
L'architecture bureau projet - Curiosité est/et intelligence